6.15 正交投影和正交补

　　小戴今天吃饱了吗注意：我们在线性变换中实际上就已经引入了投影的定义（通过核kernel和值域lm）。而在欧氏空间里，我们可以通过一个有限维的子空间和它对应的正交补来研究欧氏空间的结构。下面给出关于正交投影的定义。

　　正交投影的概念是基于正交补而给出的。而正交补的通俗理解就是：在欧氏空间V内，所有与有限维子空间U所垂直的向量的集合。（在有的教材上，正交补是通过扩充U的一组标准正交基来证明的）为了引入向量的正交投影可以直接用对应子空间U下的一组标准正交基所唯一确定，我们对定理1采用如下的证明：

　　设U是实内积空间V的一个有限维子空间，则

　　对于直和的证明，我们总是分成两部分进行。the first1： 证明V中的任意一个元素 ，存在

　　显然，为了用到正交补的性质，也为了说明 确实属于U内，我们需要用U的一组标准正交基，来实现这两个目的。

　　

　　

　　而标准正交基本身也具有很好的性质（尤其是在内积的时候），因为标准正交基中的第i个与向量的内积，就是向量在此维度下的坐标。)

　　因此，先用标准正交基表示出对应空间内的向量，就可以直接得到内积了。

　　设

　　则，立刻得到向量 有：

　　

　　( 接下来只需要证明：U和U的正交补交集为0即可。略。)

　　我们实际上是希望，能够把V中的任意一个向量，确实表示成 。在这种证明上，我们总是先把 写成和的形式，然后证明，存在符合要求的 。所以，问题是，如何证明 ?

　　这里，我们首先想到的就是正交补的等价定义： 属于U的正交补，等价于， 垂直于U中的任何一个向量。我们用标准正交来刻画这种任意性。

　　那么，此时的问题就转化成：当 时，如何说明 也是属于U的？很显然，就是结合前面设出的一组正交基。

　　强调这个证明方法的原因是，它体现了，向量的正交投影，可以通过向量与对应子空间的一组标准正交基的内积来表示。具体的应用我们将在之后给出。

　　例2:求证，欧几里得空间R^n^ 中（指定为标准内积），任一子空间U是一个齐次线性方程组的解空间。

　　review: 在线性变换里，我们是怎么处理这个问题的？- 用方程组的解来构造新的方程组，然后证明原来的系数行向量，每一个都是这个新方程组的解。

　　注意到：由于此时限定了内积，所以不可以在直接用线性空间的方法来做，因为欧几里得空间的子空间除了保持线性结构，还保持了原来定义的内积。

　　对于任意一个子空间U,都存在其正交补 且唯一，因此，设 的一组标准正交基为 ，则，对于 ,

　　取 的转置,那么

　　则， 是下列齐次方程组的解：

　　则， 属于该齐次线性方程组的解空间。

　　因此，U是齐次线性方程组的解空间。

　　在第一部分关于正交补的介绍中，已经涉及到了对于向量在具体子空间内的正交投影。对于任意维度的子空间U，给出以下的正交投影定义： 设U是实内积空间V的一个子空间，如果 ，那么有平行于 ，从V到U的投影$P_U$, 我们称投影 为V在U上的正交投影。 从最小逼近元角度的定义： 设U是实内积空间V的一个无限维子空间，如果 在U上的最佳逼近元存在（存在就一定唯一），那么把 称为 在U上的正交投影。如果V中每个向量 都有在U上的正交投影 ,那么就把它称为V在U上的正交投影。 从向量映射的的角度定义： 在正交投影 存在的前提下，我们将把 在 下的像称为 在U上的正交投影，此时， . 向量的正交投影的等价判别： 这既是判断U内一个具体的向量, 是否为已知向量 a在此平面内的正交投影的直观依据，也是我们求给定的向量在给定的子空间U上的正交投影的具体方法。表述如下：

　　

　　注：这是我们通常用来求正交投影的方法，同时，它本质上和 求子空间的正交补没有任何区别 我们回顾一下这个过程：

　　首先，求出子空间U的一组标准正交基；

　　根据正交补 (a more understandable definition: the union of all the vectors which perpendicular to the subspace U) 的定义，可知，向量与子空间U垂直，等价于向量与U的一组标准正交基垂直。（我们只是需要垂直的关系，这个时候不是标准的也没事，但是为了计算的方便，还是都化成标准的吧）。

　　正交在计算中的意义就在于：从内积为0，可以得到关于向量坐标的方程组。这样，就转化为了齐次线性方程组的求解问题。

　　通过这一例题可以加强对正交的运算性质的理解：

　　再回到最开始的正交投影的定义上，如果U是有限维的话（实际上，通常考试过程中遇到的都是有限维度的），那么，可以直接把向量在有限维子空间U上的正交投影 ,用U的一组标准正交基表示出来：

　　

　　请注意这个结果：实际上，这种坐标表示的方法非常常见，而且易于理解==投影== 的本质。（即使现在已经不再一个几何空间里了）。欧氏空间V中的向量 ，在子空间U上的正交投影，就相当于：去掉其中与U正交的部分。通过这种和几何的联系，我们给出了最小二乘解的相关表述，但是由于期末考试并不涵盖这一部分的内容，所以我不会写出具体的推导过程。

　　这也正是为什么正交投影的定义同样可以通过最小逼近元给出的原因所在。

　　设U是实内积空间V的一个子空间，则，V在U上的正交投影P满足：

　　

　　当V在W（一个子空间，可以无限维）上的正交投影P存在的时候，它就是V上的一个线性变换，而且是幂等的。同时，还有$ker(P)=W^{\bot}, lm(P)=W$

　　证明：（不要求掌握，三个部分的证明都有用到了最佳逼近元的性质。）

　　（1）证明P是V上的线性变换。

　　（2）证明P是幂等的。

　　（3）证明

　　设 是n维欧氏空间V上的对称变换，它的所有的==不同==特征值为 ,不同的特征子空间为 : V在不同的特征子空间上的正交投影，有以下结论：

　　

　　

　　而（3）、（4）实际上是一种意思：在两两正交的子空间上的正交投影，也是两两正交的。此时，就像是把对称变换分解了一样。我们看一下这种思路：

　　（4）在（3）的基础上就很显然了.

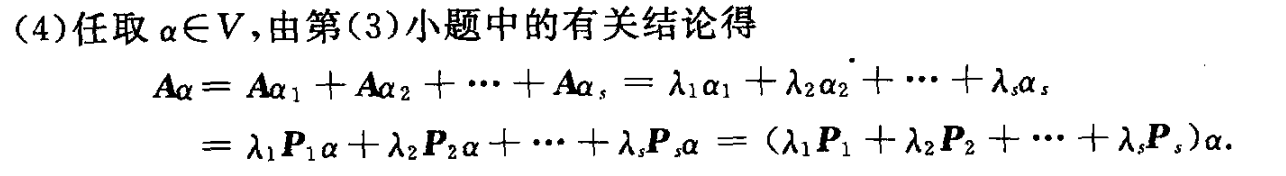
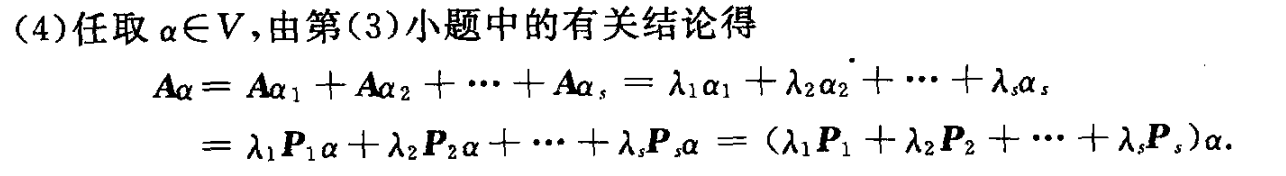　　 2020年卷2-最后一题 注1：

　　实际上，这种定义方式（对于V中的固定向量 与一个非零常数k，就能够确定一个变换 ，成为V上的对称变换。若要使得它同时成为正交变换，只需考虑线性变换成为正交变换的等价判定就好。四个等价刻画区分：正交变换和正交投影是完全不同的概念。此处问到的是正交变换，和我们已上讨论的正交投影没有关系。在更深层的理论中，实际上，投影变换和正交投影变换的区别是幂等矩阵是否是Hermite矩阵。注2:处理陌生定义下的正交变换：

　　请记住，正交变换的处理，往往就两个角度来刻画：一，是根据题中给出的定义方式，或者考虑正交变换的等价刻画，如：正交矩阵的行列向量组两两正交。 二，考虑找一组标准正交基。 2016年-第六大题 注1: 可以看到，这种定义方式实际上和2020年是重复的。同时，当固定向量选取发生变化，或者是增添系数的时候，对称变换 可能有不同的特性。例如，此处它就变成了特征值为1或-1的对称变换。

　　注2；（3）问，实际上概括了对称变换和正交投影的关系。可以如下归纳为：

　　a. ? 从对称变换到正交投影，是通过特征子空间两两正交来说明的：

　　对称变换在标准正交基下是实对称矩阵实对称矩阵一定可以对角化而线性变换可对角化就意味着特征子空间两两正交（等价判定）证明线性变换相等，只需要证明，对于任意一个向量 ,其作用效果完全一致。暗含了之前介绍过的一个结论： b. 从正交投影到对称变换，是直接说明的：因为正交投影就是原欧氏空间的对称变换。充分性证明如下：

　　正交投影是对称变换，对称变换的线性组合仍为对称变换因此，如果 是一些正交投影的线性组合，则 一定是对称变换。